백준 11726 - 2×n 타일링

C++

11726 번 - 2×n 타일링

문제

2×n 크기의 직사각형을 1×2, 2×1 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오. 아래 그림은 2×5 크기의 직사각형을 채운 한 가지 방법의 예이다.

문제 출처

접근 방법

머리가 안좋은 관계로, 일단 n이 6이 될 때까지 모든 경우의 수를 그려보니 규칙이 보여 해결 할 수 있었다.
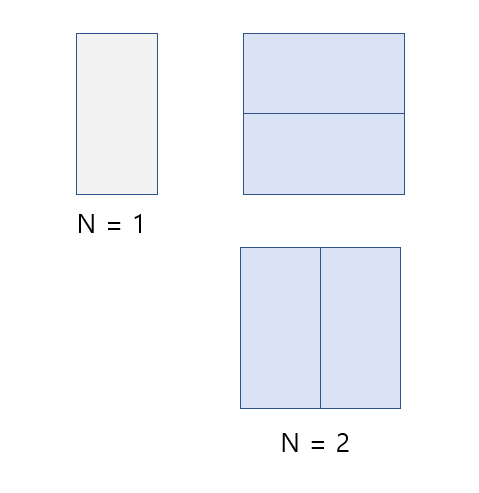
먼저 n=1와 n=2인 경우 다음과 같을 것이다.

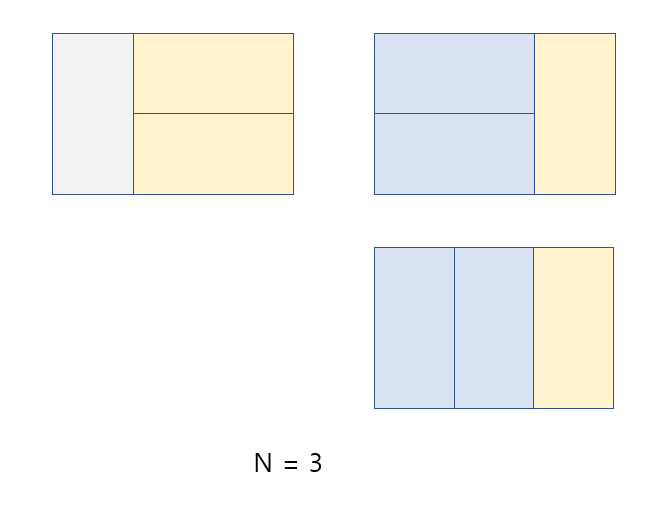
여기서 n=3와 n=4일 때를 보면 다음과 같다.

n=3과 n=4 일때의 경우를 자세히 들여다보면,
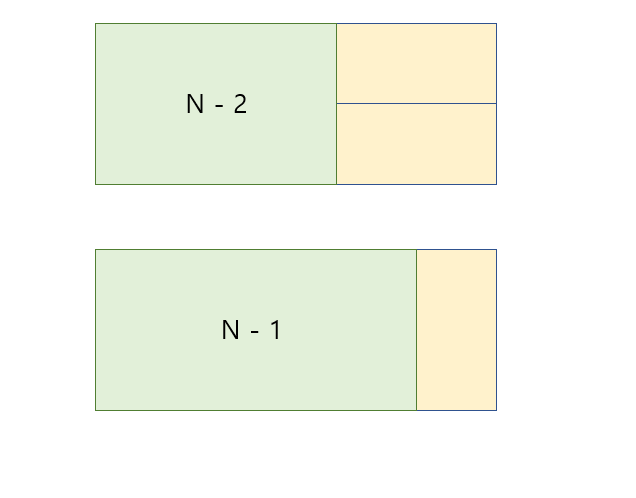
n=3일 때, n=1에서 가로로 된 직사각형 2개를 뒤에 추가하고 n=2에서 세로로 된 직사각형 1개를 추가한 것과 같다.
또한 n=4일 때, n=2에서 가로로 된 직사각형 2개를 뒤에 추가하고 n=3에서 세로로 된 직사각형 1개를 추가한 것과 같다.
이로써 n은 n-1과 n-2에서 직사각형을 각각 추가한 것의 합과 같다는 것을 알 수있다.

즉 DP로 생각하면, dp[n] = dp[n-1] + dp[n-2]로 나타낼 수 있다.

구현

dp를 이용하여 n 인덱스에서 나올 수 있는 경우의 수를 파악한다.

코드

/*
11726번 - 2×n 타일링
https://www.acmicpc.net/problem/11726
*/
#include <iostream>
#include <vector>

using namespace std;

int n;
int arr[1001];

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cin >> n;
	
	arr[1] = 1;
	arr[2] = 2;
	for (int i = 3; i <= n; i++) {
		arr[i] = (arr[i - 1] + arr[i - 2]) % 10007;
	}
	cout << arr[n];
	return 0;
}

총평

난이도

⭐⭐★★★

후기

규칙을 찾는데, 그냥 처음부터 그려보면서 확인하는게 제일 빨랐다.
역시 머리가 좋아야지 빨리 푸는 문제인가 싶다.

개선할 점

없