백준 11724 - 연결 요소의 개수

C++

11724 번 - 연결 요소의 개수

문제

방향 없는 그래프가 주어졌을 때, 연결 요소 (Connected Component)의 개수를 구하는 프로그램을 작성하시오.

문제 출처

접근 방법

주어지는 방향이 없는 그래프를 2차원 배열을 통하여 입력받는다.
이후 DFS를 통하여 해당 행에 다른 연결요소가 있으면 그 요소를 인덱스로 새로운 행을 탐색한다.
각 행을 방문 할 때마다 해당하는 인덱스를 나타내는 값을 1로 두어 방문하였다고 기록한다.
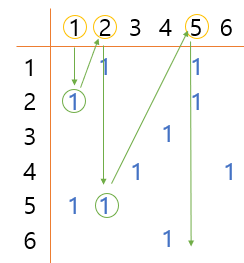
위 방법을 그림으로 나타내면,

처음 DFS는 1에서 부터 시작하므로, 1의 행을 탐색한다. graph[2][1]에 연결요소가 발견 되었으며, 2행은 방문하지 않았으므로, DFS(2)를 호출하여 새로히 탐색한다.
2행은 [2][1], [2][5]에 연결요소가 있으며, [2][1]은 1행이 이미 방문하였으므로 넘어가고, 5행으로 넘어간다.
최종적으로 1, 2, 5행을 방문하며 이는 1, 2, 5 노드가 서로 연결되어 있다는 것이다.
이로써 1, 2, 5 그리고 3, 4, 6이 연결 되어 있다는 것을 알 수 있다.

구현

1부터 n까지 DFS에 인자로 넣어 탐색을 한다. 이때 만약 한번 방문한 노드이면 DFS로 들어가지 않는다.
DFS를 완료 한 후, 총 연결 개수를 나타내는 cnt를 증가시켜준다.
즉 처음 DFS(1)로 시작하면 1,2,5 노드를 방문하므로 DFS(3)일때 다시 호출되며 이후 3,4,6으로 방문을 하여 총 cnt는 2가 된다.

코드

/*
11724번 - 연결 요소의 개수
https://www.acmicpc.net/problem/11724
*/
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

void DFS(int pos);

int n, m, cnt;
int graph[1001][1001];
bool visited[1001];

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cin >> n >> m;
	int u, v;
	
	for (int i = 0; i < m; i++) {		//방향 없는 그래프
		cin >> u >> v;
		graph[u][v] = 1;
		graph[v][u] = 1;
	}
	
	for (int i = 1; i <= n; i++) {		//1 부터 n까지 노드 방문
		if (visited[i] == false) {		//만약 처음 방문하면 == 이전 연결요소와 연결 되지 않은 노드면
			DFS(i);
			cnt++;						//연결 요소의 개수를 증가한다
		}
	}
	cout << cnt;
	return 0;
}

void DFS(int pos) {
	visited[pos] = true;			// 방문 하였으므로 true
	for (int i = 1; i <= n; i++) {
		if (visited[i] == false && graph[i][pos]) {		//현재 노드와 연결 되어있는 노드를 확인하는 조건문
			DFS(i);
		}
	}
}

총평

난이도

⭐⭐⭐★★

후기

코드는 정말 간단하지만, 위 알고리즘이 도저히 떠오르지 않아 슬펐던 문제이다.
이걸 풀면서 알고리즘 공부하는 것에 매너리즘에 빠지는 차였는데, SSAFY 과정을 통해 이제 자바로 알고리즘을 공부해야 할 것 같아 아마 마지막 c++로 정리한 코드일 것 같다.
가슴이 아프지만, 받아드려야지

개선할 점

또 보자 c++