백준 2617 - 구슬 찾기

Java

2617 번 - 구슬 찾기

문제

모양은 같으나, 무게가 모두 다른 N개의 구슬이 있다. N은 홀수이며, 구슬에는 번호가 1,2,…,N으로 붙어 있다.
이 구슬 중에서 무게가 전체의 중간인 (무게 순서로 (N+1)/2번째) 구슬을 찾기 위해서 아래와 같은 일을 하려 한다.

한 쌍의 구슬을 골라서 양팔 저울의 양쪽에 하나씩 올려 보면 어느 쪽이 무거운가를 알 수 있다.
이렇게 M개의 쌍을 골라서 각각 양팔 저울에 올려서 어느 것이 무거운가를 모두 알아냈다.
이 결과를 이용하여 무게가 중간이 될 가능성이 전혀 없는 구슬들은 먼저 제외한다.

M 개의 쌍에 대한 결과를 보고 무게가 중간인 구슬이 될 수 없는 구슬의 개수를 구하는 프로그램을 작성하시오.

접근 방법

DFS를 사용하여 그래프 탐색으로 해결하였다.
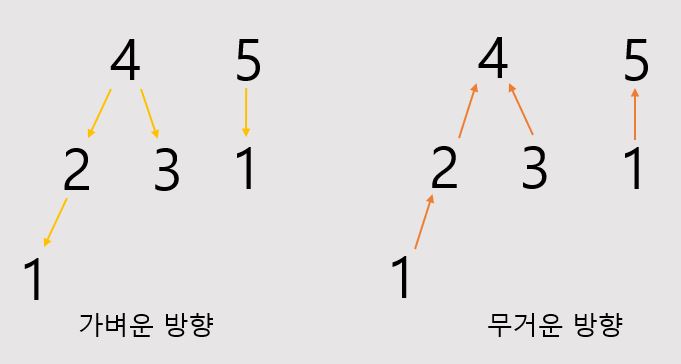
각 구슬의 무게 대조한 값을 단방향 그래프로 나타낸다.
구슬 2번이 구슬 1번보다 무겁다. : 2 -> 1
구슬 4번이 구슬 3번보다 무겁다. : 4 -> 3

1부터 n까지의 구슬 각각을 시작으로 DFS로 타고 들어가 만나는 구슬의 개수를 구한다.

[자신보다 가벼운 구슬의 수]가 [전체 구슬의 수 / 2 + 1] 보다 크다면 무게가 중간이 될 가능성이 전혀 없는 구슬이 된다.

이제 반대 상황인 자신보다 무거운 구슬의 수도 세어, 무게가 중간인 구슬이 될 수 없는 구슬의 총 합을 구한다.

코드

import java.util.*;
import java.io.*;

public class Main {
	static int n, m, result, downCnt, upCnt;
	
	static boolean[][] up, down;
	static boolean[] upVis, downVis;
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    	StringTokenizer stk = new StringTokenizer(br.readLine());
    	n = stoi(stk.nextToken());
    	m = stoi(stk.nextToken());
    	
    	up = new boolean[n+1][n+1];
    	down = new boolean[n+1][n+1];	
    	
    	int big, small;
    	for(int i = 0; i < m; i++) {
    		stk = new StringTokenizer(br.readLine());
    		big = stoi(stk.nextToken());
    		small = stoi(stk.nextToken());
    		down[big][small] = true;	// 무거운 구슬에서 가벼운 구슬로
    		up[small][big] = true;		// 가벼운 구슬에서 무거운 구슬로
    	}
    	
    	int bound = (n / 2) + 1;		// 중간이 될 수 없는 경계 값
    	for(int i = 1; i <= n; i++) {
    		init();
    		FindDown(i);				// 현재 구슬보다 가벼운 구슬을 찾는다.
    		FindUp(i);					// 현재 구슬보다 무거운 구슬을 찾는다.
    		if(upCnt >= bound || downCnt >= bound)
    			result++;
    	}
    	
    	System.out.println(result);
    	
    	br.close();
	}
	// 구슬 방문여부, 개수 초기화
	private static void init() {
		upVis = new boolean[n+1];
    	downVis = new boolean[n+1];
    	upCnt = 0;
    	downCnt = 0;
	}
	// 시작 구슬부터 더 가벼운 구슬들을 찾는다
	private static void FindDown(int num) {
		for(int i = 1; i <= n; i++) {
			if(down[num][i] && !downVis[i]) {
				downVis[i] = true;
				downCnt++;
				FindDown(i);
			}
		}
	}
	// 시작 구슬부터 더 무거운 구슬들을 찾는다
	private static void FindUp(int num) {
		for(int i = 1; i <= n; i++) {
			if(up[num][i] && !upVis[i]) {
				upVis[i] = true;
				upCnt++;
				FindUp(i);
			}
		}
	}

	static int stoi(String str) {
    	return Integer.parseInt(str);
    }
}

총평

후기

DFS를 사용하여 그래프를 탐색하는 방법에 대하여 부족하다.
그래프 이론에 대하여 공부를 많이 할 필요가 있다.

개선할 점

플로이드 워셜로도 풀어봐야한다.